Arkay Firestar
Very Active Member
- Joined
- Apr 28, 2010
- Messages
- 245
Man the clear prototype still looks the best.
I'd hope so, since there's still a year until that happens (if you believe that we really started counting at year 1 AD)I'm so excited! There's a chance we will all get our Pyras before the end of the decade!
You at risk of confusing offsets with numbers, which seems to be an oft-occuring problem amongst programmers?I'd hope so, since there's still a year until that happens (if you believe that we really started counting at year 1 AD)
Then you should have a look atHaven't had a new update in a while.
The latter I'd call the second decade of this century. The 20-10s I'd call the years matching /201[0-9]/. But that's just me. I don't know what the norm says. And I don't remember what my point was writing my last comment.Are you sure? If the decades run contiguous from the start, they would begin at the start of 1 CE and run to the end of 10CE, making ten whole years. So the next would be 11CE to 20CE, and the current one would be Jan 2011 to Dec 2020.
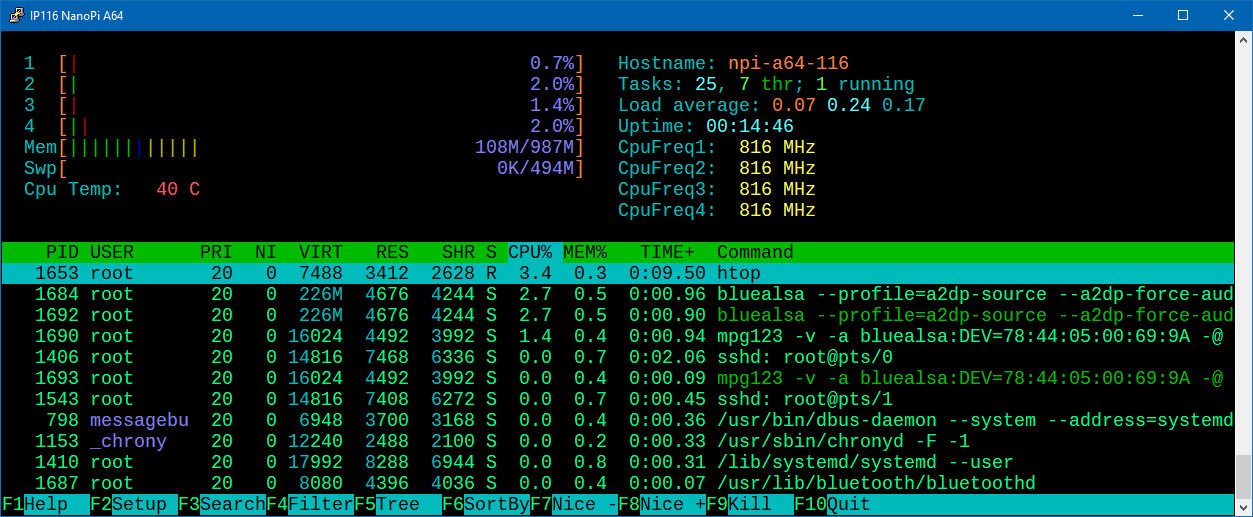
One of the main reasons PulseAudio is being used is the ability to configure Bluetooth audio devices on the fly, if it doesn't support that we could just as well go back to full ALSA.Looks like sndio may be a way to have a clean audio:
The prototypes have gone out, and they are starting to be received and worked with. That is pretty big news, imo.Haven't had a new update in a while.
Seem to be a lot of fiddling around for the end user.Why shouldn't it be possible ?

BlueALSA: Bluetooth-Audio using ALSA (not PulseAudio)
Yesterday I did get a new little Bluetooth-Speaker, but without AUX - I rechecked some Bluetooth-Commands. But could never connect, because the Pi missed the protocol A2DP - which was only available with PulseAudio as Bluetooth-Module So I used my 2nd OrangePi One with USB-Bluetooth-Dongle and ma...forum.armbian.com
You should not talk like a troll about these people who are very respectful of the free software movement. Shame on you.and it certainly never does any of the bullshit they talk about there.
Seems only a user-space tweaking, at least it's worth investigating.Seem to be a lot of fiddling around for the end user.
It looks like you need to choose the alsa audio device each time you want to play audio to speaker / headphone / bluetooth.
With Pulseaudio, you can redirect the stream on-the-fly, which is a huge advantage.
We have to keep opensource open, and free software free.I think some of us are trying to avoid pulse and friends.

