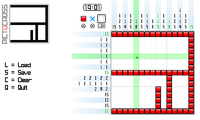
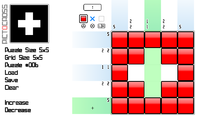
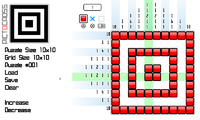
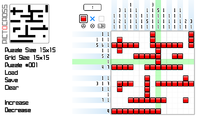
Hmm, it'd certainly be possible to brute-force the puzzles and see if they're completable from the clues, but I'd expect there to be a more efficient way to do it.
In practice when I do a puzzle like this I look for the longest lines first, e.g. if it's a 15x15 puzzle I'll look for a line that's say 7 and 6 making a total of 14 (7+6+1). Big numbers help because then even if the line's two or more short, as long as the piece is three or more long there's always be an overlap that's guaranteed to be set.
That's pretty much all the logic there is to these puzzles. Setting crosses is important too I guess, as they puts extra constraints on shorter lines and lets you work out where they could fit I guess. If a line is a 1, 1, 2, 3, 1 and you find three in a row set you know that's the three and can terminate it with crosses. Hmm, though that also tells you where the three is in the line, and say that's towards the left of the puzzle can fix the position of the 1, 1 and 2 too. That's a little trickier to encode as an algorithm, I suspect. Or maybe it has a recursive solution, as once you can split the clue and the puzzle at a point, you can feed the shorter clue and the shorter puzzle line into the original algorithm that works out if whole lines can be guessed in the puzzle.
Hmm, I get the feeling I'm disappearing down a logical rabbit hole here, so I'll have to leave it there for a bit.