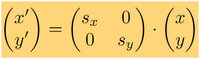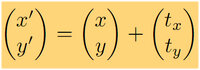Programmierproblem, bedingt durch Mathematik

[boeseronkel2k]

Liebe Community,
ich hab ein kleines Programmier Problem welches aber garnicht programmiertechnisch bedingt ist sondern,
leider bedingt durch meine nicht vorhandenen Mathematik-Fertigkeiten

Fang ich einmal an:

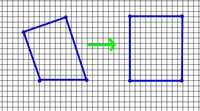
Ich habe 4 eckpunkte eines Vierecks (kann Quadratisch, Rechteckig, Trapezförmig, Rautenförmig sein),
nennen wir sie P1, P2, P3, P4

P1 ist Oben Links

P2 ist Oben Rechts

P3 ist Unten Rechts

P4 ist Unten Links


Nun möchte ich das ganze mittels einer Transformationsmatrix da draus ein Rechteck machen,
das Wrappen mit der Transformationsmatrix kann die OpenCv wunderbar machen, aber leider hilft
die mir nicht bei meinem Problem, dass ich erst eine Matrix berechnen muss und ich keine Ahnung habe,
wie ich das denn zu tun habe

Ich hoffe ihr könnt mir helfen ohne dass ich noch öfters mit meinem Kopf auf die Tastatur hauen muss in der hoffnung,
dass mir eine Idee kommt....
Oder hat vielleicht einer von euch nen schönen Ansatz dazu?

in bester Hoffnung,
b2k

 

[relei]

Hi,

kannst du dein Vorhaben kurz skizieren?

Schönen Gruß
Rene

 

[torro]

Am einfachsten geht es glaube ich, wenn du dein Viereck zuerst in ein Einheitsquadrat transformierst. Das geht einfach indem du dir anschaust, wie die Einheisvektoren nach der Trafo abgebildet werden und der Nullpunkt verschoben wird. Nun musst du nur noch die Inverse dieser Trafo bestimmen und du hast es. Wenn du kein Einheitsquadrat haben möchtest, ist der Weg darüber wohl trotzdem am einfachsten (bestimmt nicht am schnellsten) wenn du anschließend noch eine zweite Trafo durchführst.

Nicht so einfach zu erklären ohne Bild, falls du es nicht kapierst kann ich es dir vielleicht noch aufmalen.

 

[boeseronkel2k]

Ich hab hier das Vorhaben einmal skizziert,

Die Transformation in ein Einheitsquadraht wär ganz gut, ich glaube da muss ich mich mal einlesen

Hast du eventuell noch Informationen dazu?

 

[torro]

Ok, ich habe das Problem falsch verstanden, mein Ansatz geht nur für Trafos, die aus Rotation, Scherung, Skalierung und Verschiebung zusammengesetzt sind. Bei dir ist das ja keine affine Transformation mehr, da hab ich so spontan auch keinen Ansatz. Ich hab mal so morphingsachen mit Federausgleichsmodell ralisiert, aber das ist natürlich unglaublich rechenintensiv.

 

[boeseronkel2k]

falls es hilft, es muss nicht 100% ig sein,
meine idee wäre:

höhe und breite berechnen (pythagoras, je links / oben, rechts unten und mittelwert nehmen)
und dann inhalt drehen (winkel wieder mittel aus links/oben und rechts/unten)

aber kennt da jemand nicht ne bessere möglichkeit

 

[Holliefant]

Nur ne doofe frage, muss das neue Viereck genauso groß sein wie das alte?
Oder liege ich hier komplett falsch?


Wenn Ja dann hierrüber:

http://de.wikipedia.org/wiki/Gau%C3%9Fsche_Trapezformel

und dann ein Quadrat daraus berechnen solle nun wirklich kein Problem sein

 

[boeseronkel2k]

Das ist egal, soll hinterher eh nach 16*16 downgesampled werden, zum füttern eines Neuronales Netzes

 

[Holliefant]

sry ich blicke nicht was du meinst, bin wohl zu doof dafür

 

[boeseronkel2k]

dann muss ich wohl doch ein bischen ausführlicher werden:

Es geht darum, dass Zahlen auf Schildern erkannt werden müssen, diese Schilder sind Rechteckig,

Diese Schilder werden durch eine Kamera aufgenommen.

Da die Schilder vierteckig sind, ist deren erkennung (Canny, 4 Linien, welche sich Kreuzen) relativ einfach,

nun habe ich die 4 Eckpunkte,

nun nehme ich (momentan) das kleinstmögliche Rechteckt in dem Bereich zwischen den 4 Eckpunkten.

ascii art Beispiel:

[ 1 ]

Jedoch ist das Problem, dass wenn es schräg erkannt wird, dass es eher ausschaut wie eine
___
/ 7 /
---

Daher dachte ich, wäre eine Transformation ganz Praktisch um die Perspektive zurück zu setzen.


(zu guter letzt wird mit den Pixelwerten ein Künstliches Neuronales Netz gefüttert, welches mir ausspuckt welche
Nummer erkannt wurde...)

Jedoch treten bei 7 und 1 durch die geänderte Perspektive große Probleme bei der Erkennung auf.

Nun wär meine Idee die Perspektive herausrechnen zu lassen, damit die Zahlenerkennung auch hier klappt.

[edit]und da die Erkennung der Quadrahte nicht 100%ig ist, könnte also diese Raute auch ein Trapez oder sonnstiges sein[/edit]

Da ich jedoch kaum eine Idee habe wie ich dort heran gehen soll, bin ich um jeden Strohhalm zum analysieren und begutachten für das Problem dankbar.

Viele Grüße,
b2k
Im Idealfall, bedingt durch

 

[JohnDavidson]

Besitzt du Informationen im 2D oder im 3D Raum? Ich gehe mal von 2D aus. Du solltest dich auf jeden Fall nach dem Thema Computergrafik + Transformation umschauen.

Habe mal was angehangen, damit du dich einarbeiten kannst
Und bei der Berechnung musst du erstens beachten, das Rechteck seinen Mittelpunkt im Nullpunkt des Koordinatensystems hat. Und dass die Multiplikation der Matrizen in der Umgekehrten Reihenfolge stattfindet, als man denkt.
Sprich wenn du erst eine Translation (T) in den Null-Punkt machen möchtest und dann erst die Rotation (R), dann musst du folgendes berechnen:
R*T

Ich hoffe ich konnte dir nen kleinen Denkanstoss geben

 

[boeseronkel2k]

Vielen dank, JD

klappt hervoragend

 

[SebuSoft]

Vielen dank, JD

klappt hervoragend

<- war dir damit den schon geholfen?

Denn den ich hätte jetzt mehr damit gerechnet das du die 2D Punkte dafür erstmal in Homogene 3D Punkte umwandeln musst (einfach zu jedem 2D Punkt den w Wert: 1 hinzufügen) und sie dann mit Hilfe des DLT Verfahrens in eine Homographie-Matrix umwandeln kannst.

Dann könntest du jeden 2D Punkt im einen Quadrat einfach in einen Homogenen 3D Punkt umwandeln (s.o.) mit der H-Matrix multiplizieren und den Punkt Homogenisieren (jeden Wert x,y und w durch den w Wert teilen) und dann hätte man den entsprechenden Punkt (w Wert ignorieren ist dann ja 1) im 2. Quadrat.

Im übrigen ist so eine Homograpie eine Matrix welche die 3 Matrizen von JohnDavidson kombiniert und auch Perspektivische Verzerrungen behandelt.

Mit Hilfe des DLT-Verfahrens kann man halt aus den Punkten die gesuchte Matrix berechnen. (funktioniert im übrigen auch mit 3D oder noch mehrdimensionalen Punkten, werden aber um eine Dimension w größer und man benötigt logischerweise mehr Punkte um die Matrix zu ermitteln)

Auf die Art und Weiße könntest du die Schilder zumindest mit Hilfe der Eckpunkte völlig entzerren und hättest so einigermaßen saubere Eingaben für dein Neuronales Netz.

etwa so:

Spoiler

 

[boeseronkel2k]

Jain

Ich wusste wonach ich suchen musste und habe eine fertige Funktion in der OpenCV gefunden,

cvGetPerspectiveTransform()

Der gibts man 8 Punkte,
4 Die die das source Rechteck beschreiben
und 4 die es nach der Transformation beschreiben

Und er Berechnet einem eine 3x3 Matrix zum Warpen

Also genau das was ich gesucht habe, wenn auch nicht selber implementiert, aber zumindestens läuft es

[edit]
gemäß http://en.wikipedia.org/wiki/Direct_linear_transformation würde ich sagen, die OpenCv Funktion implementiert DLT
[/edit]